ACCURATEZZA E PRECISIONE DELLA QUOTA ORTOMETRICA NEI RILIEVI SATELLITARI GNSS
Ok. Lo so. Hai letto il titolo dell’articolo ed hai subito storto il naso. Sembra che al suo interno ci siano delle incongruenze. Accuratezza=precisione? Satellitari=GNSS? Quota ortometrica o altezza ellissoidica? Ora vi spiego…
Tutto è nato da una chiacchierata con un paio di tecnici a proposito della determinazione della quota ortometrica dei punti rilevati con una strumentazione satellitare. Uno diceva che le quote ottenute non sono per niente affidabili e l’altro riportava addirittura errori quantificabili in 30 cm ed oltre. Siamo tutti d’accordo sul fatto che le attività pertinenti alla misura delle quote siano le livellazioni e non i rilievi satellitari (in realtà in topografia si misurano i dislivelli e poi si deducono le quote attraverso dei caposaldi di livellazione), tuttavia non mi sentirei di dire che le quote dedotte da misure satellitari siano del tutto da buttare. Dipende da cosa devi farci. Stai facendo un monitoraggio di una struttura? Stai facendo un rilievo plano-altimetrico di un versante? La prova che ti descriverò nel seguito ti aiuterà nel decidere se utilizzare un livello o una strumentazione satellitare a seconda dell’accuratezza che vorrai ottenere dal tuo rilievo.
Lo strumento satellitare non lo chiamerò semplicemente GPS perché in realtà, come sappiamo, ci sono anche altre costellazioni di satelliti che vengono rese disponibili per gli scopi civili. La mia strumentazione, ad esempio, capta anche i segnali della costellazione GLONASS. Quindi mi riferirò alla strumentazione satellitare o GNSS (Global Navigation Satellite System) indifferentemente e non alla GPS in particolare.
Inoltre, mi riferirò all’accuratezza per descrivere quanto la misura sia vicina al suo valore reale (o assunto come tale), mentre la precisione si riferisce alla ripetitività della misura. Le misure sono precise quando si discostano poco l’una dall’altra, ma magari sono lontane dal valore reale e quindi sono inaccurate.
Veniamo alla prova. Lo scopo è quello di confrontare la quota ortometrica dedotta dall’elaborazione di un rilievo GNSS con quella ottenuta riferendosi ai caposaldi di livellazione IGM. Operativamente la prova si è svolta nel seguente modo:
- Ho scelto 10 caposaldi appartenenti alla rete di livellazione di alta precisione dell’IGM e mi sono scaricato le monografie. Non mi sono spostato molto, infatti li ho scelti tutti nell’intorno di 15 Km dal mio ufficio ed erano disposti lungo una strada statale ad intervalli di circa 1 Km.
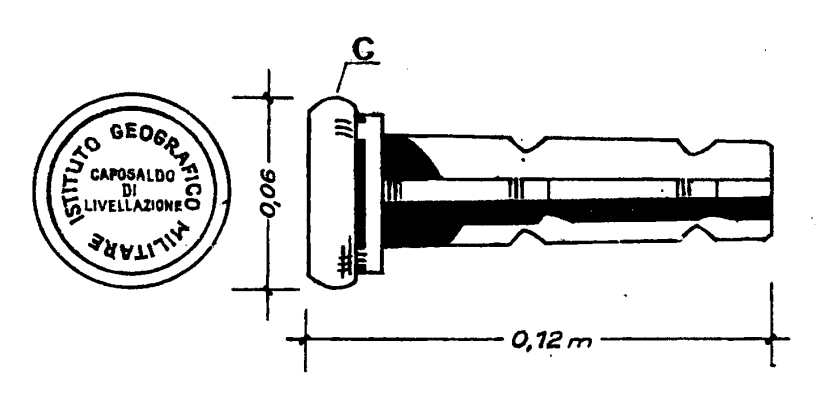
I caposaldi, in genere, sono materializzati con dei “bulloni” in ghisa cementati su una parete verticale (infatti servono per determinare le quote, non le posizioni planimetriche…) o con dei centrini di superficie.

- Scostandomi dal caposaldo, ho rilevato un punto con lo strumento GNSS. Ho dovuto spostarmi perché i caposaldi, essendo fissati a parete, non erano direttamente rilevabili appoggiandoci sopra la punta della palina e la misura GNSS sarebbe probabilmente stata influenzata dall’effetto del multipath del segnale. I centrini di superficie, al contrario, ho potuto rilevarli in questo modo. La palina era tenuta in posizione dal bipiede e prima di rilevare il punto ho atteso circa 5 minuti. Ogni punto lo ho rilevato 10 volte ad intervalli di circa 5 secondi. Lo strumento era un Leica 1200+ ed il rilievo è stato condotto in modalità NRTK ricevendo le correzioni differenziali dalla rete di stazioni permanenti TPOS della Provincia Autonoma di Trento. Ho utilizzato il mountpoint IMAX3 e la baseline aveva una lunghezza massima di circa 15.3 Km. La giornata era uggiosa e ad un certo punto ha cominciato anche a piovere. L’indice Kp, indicatore dell’attività geomagnetica terrestre, aveva un valore di 1 su una scala di 9, quindi un valore ottimale. Il numero di satelliti acquisiti era variabile tra 9 e 13.
- Durante i 5 minuti nei quali l’antenna rimaneva immobile in posizione sul punto, ho rilevato il dislivello tra il caposaldo di livellazione ed il punto battuto. Mi sono servito di un livello laser Leica Lino L2 avente una precisione di livellamento di +-1 mm ogni 5 m (dichiarata dal costruttore).

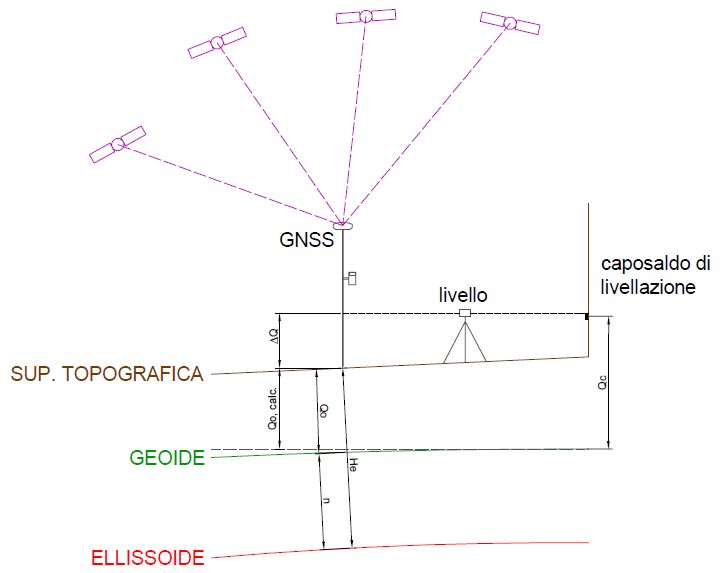
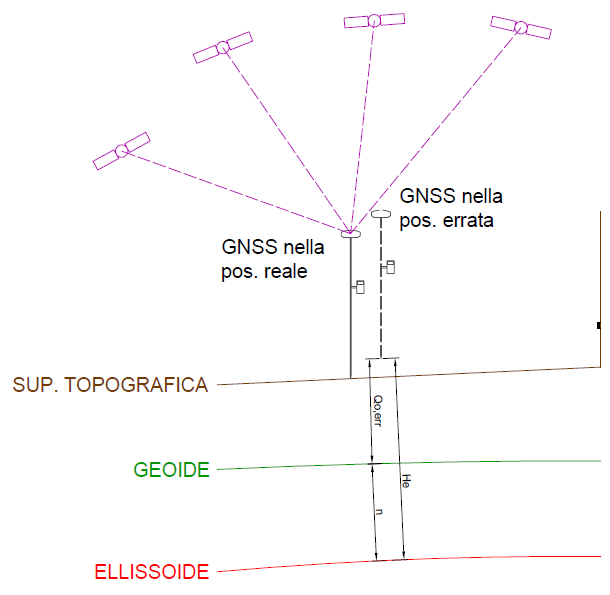
- Facendo riferimento all’immagine seguente, la quota ortometrica del punto battuto (Qo,calc) è data dalla quota del caposaldo (Qc) meno il dislivello (delta Q). Va detto che, nella trattazione delle misure, ho considerato il geoide come una superficie orizzontale nell’intorno del caposaldo (linea grigia tratteggiata). Questo in virtù del fatto che la distanza tra caposaldo e punto battuto era al massimo di una decina di metri. Teoricamente, nel punto battuto, la quota ortometrica sarebbe quella che ho indicato con Qo in figura.
- Terminato il rilievo dei 10 caposaldi ho elaborato i dati utilizzando come sistema di riferimento cartografico l’ETRF2000, per la posizione planimetrica, e le quote ortometriche dedotte dai grigliati .gk2 forniti dall’IGM. Visto che ogni punto vicino al caposaldo è stato rilevato 10 volte, ho ottenuto 10 valori della quota ortometrica dei quali ho calcolato la media aritmetica e lo scarto quadratico medio. Non ho escluso nessuna delle misure acquisite, quindi la media è stata calcolata utilizzando tutti i dati, anche quelli estremi.
Nell’immagine seguente puoi vedere un estratto del foglio Excel che ho utilizzato per analizzare le misure. Se ti interessa, puoi scaricarlo in fondo all’articolo.
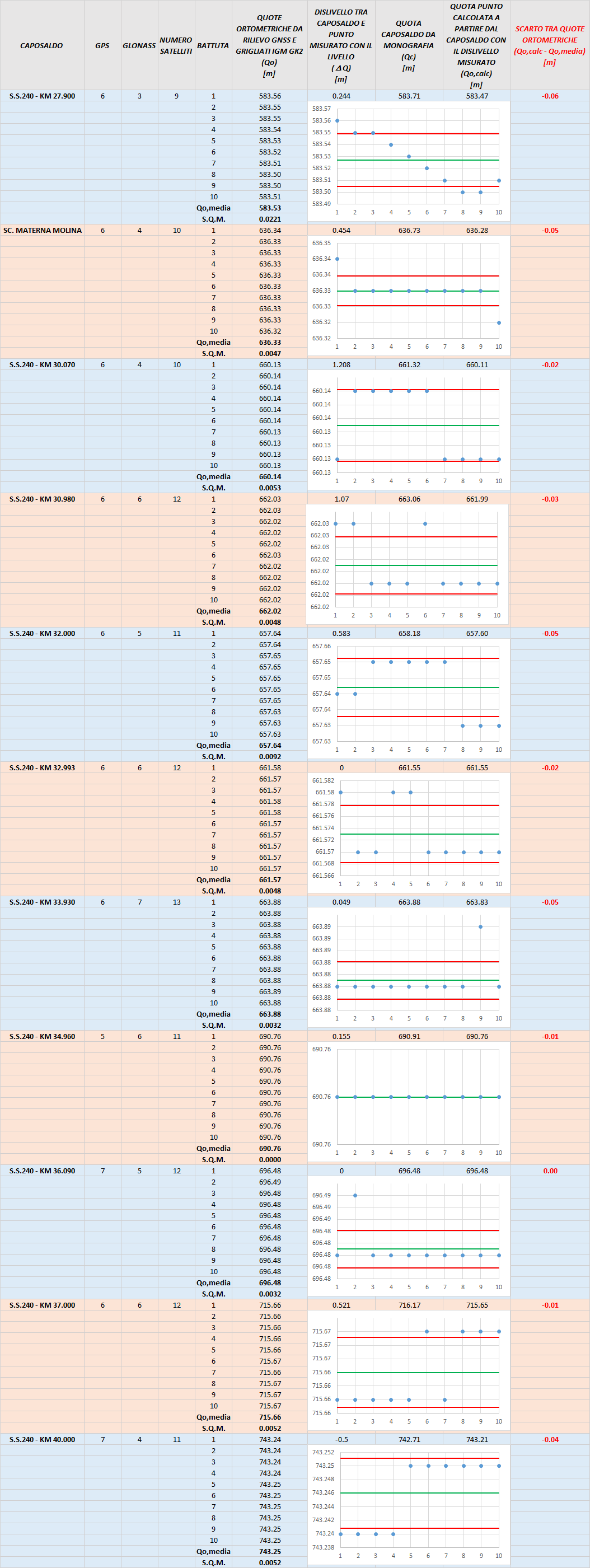
Dall’analisi dei risultati è emerso che l’accuratezza delle quote ortometriche è variabile tra un -6 cm e 0 cm (colonna in rosso). Nei grafici ho riportato con dei pallini blu le quote ortometriche dedotte da ogni singola battuta, in verde il loro valore medio ed in rosso i limiti dello scarto quadratico medio. E’ interessante notare come, nel caso del primo caposaldo, le battute tendessero a “fluttuare” attorno al valore medio. Probabilmente, se avessi continuato le misure, si sarebbero attestate su tale valore. La quota di questo caposaldo è risultata essere la meno accurata.
Nel caso del caposado SC. MATERNA MOLINA, le misure presentano una buona ripetitività, tranne la prima e l’ultima. I valori sono tutti contenuti entro 2 cm di scarto.
Nel caso del caposaldo posto al KM 30.070, le misure saltano da un valore all’altro, ma la loro differenza è di 1 cm, quindi la causa dei continui salti è da ricercarsi nella precisione strumentale. Parliamo di 1 cm visto da 20.000 Km di distanza!
Per il caposaldo al KM 34.960 tutte le misure sono uguali.
Analisi simili possono essere condotte per gli altri punti nei pressi degli altri caposaldi.
Per correttezza va detto anche che la livellazione che ho eseguito con il livello laser per calcolare la quota dei punti partendo da quella del caposaldo, non è certo una livellazione di alta precisione. Lo stesso raggio laser ha uno spessore di 2-3 mm. Comunque sia, direi che i risultati non sono male. Ripeto. Dipende cosa devi farci con queste misure. Se ne avete la possibilità, fate sempre un controllo delle quote del rilievo trasportando la quota di un caposaldo. Gli errori che potrebbero influenzare i risultati del vostro rilievo non sono tanto quelli legati all’elaborazione o alla cattiva interpolazione dei grigliati IGM per dedurre la quota ortometrica. In genere i software interpolatori (Convergo, Topko, Meridiana, ecc.) restituiscono tutti dei valori simili; differiscono al massimo di 4-5 mm. L’errore potrebbe invece riguardare la determinazione dell’altezza ellissoidica (He nell’immagine riportata sotto). Se i disturbi ionosferici sono elevati, se la baseline è troppo lunga, se interviene il cosiddetto multipath, se la distribuzione dei satelliti non è ottimale, ecc., potresti ottenere delle coordinate geografiche poco accurate ed allo stesso modo anche un’altezza ellissoidica inaccurata. Da essa, sottraendo l’ondulazione del geoide (n), viene calcolata l’altezza ortometrica.
Se ti va di approfondire l’argomento riguardante il campo gravitazionale terrestre ed i modelli di geoide, puoi leggere un altro mio articolo e visionare il video ad esso collegato.
Ti ricordo che mi trovi anche su Telegram (https://t.me/giampaoloberetta) dove ho aperto un canale nel quale ti parlo della mia attività e condivido informazioni (https://t.me/inggiampaoloberetta).
Ciao!



Molto interessante ..e complimenti per la voglia di sperimentare :-)
Una osservazione : dalla foto del caposaldo, asta antenna GNSS e raggio laser del livello, sembra che la quota del caposaldo sia stata considerata al CENTRO del bullone ..
La quote sono in realta’ sulla TANGENTE SUPERIORE della superficie toroidale del bullone ..
Piercarlo
Ciao e grazie dei complimenti. Credo che sperimentare e provare sia una fase molto importante del lavoro, sia per quanto riguarda l’apprendimento di qualcosa di teorico, sia per imparare ad usare un nuovo strumento di lavoro. Grazie ancora.
Articolo estremamente interessante, mi associo seppure tardivamente nei complimenti e nei ringraziamenti.
Prendo in parola l’osservazione che è stata fatta riguardo al punto da ritenersi quotato in questo particolare tipo di capisaldi verticali “a bullone”, che indubbiamente è (ma mi pare non ci fossero dubbi) superiormente al “colletto”, per provare a porre da non Tecnico (sono un Archeologo) a mia volta un quesito: va bene che si tratta di una ovvietà ma dove facciamo riferimento per affermare ciò?
Non trovo mai esplicitata questa pur ovvia indicazione nella documentazione dell’IGM della quale io sia a conoscenza nè in quella dei numerosi enti di Regioni e persino Comuni che hanno adottato nel tempo questo tipo di caposaldo per le proprie reti di livellazione.
Se ci fossero suggerimenti, ne sarei ben grato!
Ciao, complimenti innanzitutto per l’articolo chiaro e per la sperimentazione accurata, è proprio l’articolo che stavo cercando!
Un argomento che mi sta particolarmente a cuore, perché spesso mi occupo di regimazioni idrauliche in cui mi capita di dover prevedere cosa possa succedere in caso di rottura degli argini, è come determinare con certezza la quota reale di punti noti, perché differenze altimetriche anche piccole possono far variare drammaticamente la direzione di flusso delle acque.
Nella sequenza dei punti da te verificati ho notato che gli scarti rispetto al valore nominale del caposaldo, in centimetri arrotondanti, sono i seguenti: 20, 40, 120, 100, 50, 2, 0, 15, 0, 50, -55.
A fronte di una buona precisione, intesa come ripetitività della misura secondo la tua definizione, compresa entro una variabilità di 6 cm, mentre l’accuratezza, intesa come valore assunto come “reale” in base al caposaldo dell’IGM, presenta variazioni da -55 cm a +120 cm, pur a distanze relativamente modeste tra caposaldo e caposaldo, dell’ordine del chilometro come da te descritto.
Ora, dacché lavoro spesso con l’interpretazione di aerofotografie riprese da drone e rimontate in modelli 3D di elevato dettaglio, mi capita talvolta di posare dei riferimenti a terra, nell’ambiente detti Ground Point, e batterli con la mia stazione totale per poi utilizzarli per correggere eventuali errori marginali nell’interpretazione automatizzata delle fotografie aeree, che hanno coordinate GPS nei dati EXIF e vengono scattate in gran numero, spesso oltre mille foto per ogni sito.
Mi sarebbe infinitamente più comodo, però, rilevare una quota precisa su alcuni punti poi riconoscibili nelle foto aeree ed assegnarla come vincolo per correggere possibili curvature planimetriche.
Il dubbio che mi rimane, però, è quale sia l’accuratezza di misure altimetriche prese con una strumentazione di qualità, non vorrei mai introdurre errori dovuti alla poca accuratezza dello strumento, magari di un ordine di grandezza maggiore rispetto a quello ottenuto dall’interpolazione di migliaia di foto georeferenziate.
La mia domanda, quindi, è la seguente: la differenza di un metro e venti tra la quota di 660,13 del GPS e di 661,32 dell’IGM è dovuta a un errore intrinseco del sistema GPS, non suscettibile di correzione, o al fatto che quando l’IGM ha rilevato il caposaldo la strumentazione era molto più imprecisa di quella odierna, e quindi ha ragione il GPS?
Grazie e complimenti ancora per l’articolo!
Ciao e grazie per gli apprezzamenti.
Forse nella spiegazione non sono stato molto chiaro, ma dal foglio Excel si capisce meglio. La quota di 660.13 m non è quella del caposaldo, ma quella di un punto vicino. La misura GNSS è stata ripetuta 10 volte e poi mediata ottenendo 660.14 m. La quota del punto battuto col GNSS è stata poi dedotta da quella del caposaldo (661.32 m) semplicemente deducendo il dislivello (1.208 m) tra il caposaldo ed il punto battuto ottenendo 660.11 m. Quindi la quota del punto rilevato vale 660.14 m (come media tra le 10 misure GNSS) e vale 660.11 m se trasportata dal caposaldo. La differenza tra le due è di soli 0.03 m e non di 1.2 m. L’IGM ha aggiornato di recente le quote dei caposaldi effettuando delle misure gravimetriche molto accurate. Il mio esperimento è stato fatto con strumentazioni semplici e metodi semplici. Per essere più accurati si sarebbe dovuta eseguire una livellazione dal mezzo con un livello ottico e un rilievo GNSS statico anziché nRTK. Comunque, i risultati sembrano essere comunque buoni. Poi, naturalmente, dipende da cosa deve farci uno con tali quote.
Ciao.